'Attention is all you need' 논문 리뷰

선정 배경

• 최근 AI 산업에서 가장 화두로 떠오른 LLM뿐만 아니라, Computer vision, Recommender System 등 여러가지 분야에서 Transformer기반의 모델들이 준수한 성능을 보이고 있는 가운데, Transformer의 등장 배경과 그 자세한 원리를 파악하고자 리뷰를 작성하게 되었습니다.

Abstract

Transformer는 Attention 메커니즘으로만 구성된 모델로서, recurrence와 convolution 연산 과정 없이 구성된 모델이라고 할 수 있다. WMT 2014 English-German 번역 task에서 Transformer는 28.4 BLEU로 기존의 SOTA에 비해 2BLEU 뛰어난 성능을 보이기도 했다.

• BLEU : Generated Sentence의 단어가 Referenced Sentence에 포함되는 정도
• ROGUE : Referenced Sentence의 단어가 Generated Sentence에 포함되는 정도

Intro

Recurrent 모델들은input, output에 해당되는 토큰을 순차적으로 연산하도록 고안되었기 때문에, Training Sample에 대한 병렬화(Parallelization)을 배제할 수 밖에 없도록 설계되었고, Sequence가 길어질수록 메모리적, 시간적으로 효율성이 떨어지게 된다.

 

또한, RNN, LSTM, GRU와 같은 기존 Sequential, Transduction 모델은 시퀀스가 지날수록 이전 시퀀스의 정보가 소실되는 문제가 발생하게 되지만, Attention 메커니즘을 사용한 모델의 경우에는 Input, output 시퀀스간의 거리, 의존성에 상관없이 연산이 가능하기 때문에, Attention 메커니즘은 sequential, transduction 모델의 필수적인 요소로 자리잡게 되었다.

 

이런 장점에도 불구하고, 몇몇의 모델만이 기존의 Recurrent 구조와 Attention을 함께 사용할 뿐이므로 , 해당 논문에서는 Attention 메커니즘만을 사용한 Transformer를 제안하고 있다.

Model Architecture

Transformer는 input sequence를 latent화 시키는 Encoder, latent vector를 실제 식별가능한 output으로 해석해내는 Decoder로 이루어져 있다,

Encoder

Encoder의 경우는 크게 1) Self-Attention 2) FFN으로 구성된 Layer를 중첩시킨 구조로 이루어져 있다.
해당 논문에서는 Layer의 수를 6으로 놓고 설계하였다.

1. Self-Attention
   • Multi-headed Self attention으로 input embedding data에 대한 연산 진행
   • Residual Connection (Skip Connection)
   • Layer Normalization
     • $\rightarrow \text{LayerNorm}(x + \text{Sublayer}(x))$
2. FFN
   • Position-wise FC Layer
   • Residual Connection (Skip Connection)
   • Layer Normalization
     • $\rightarrow \text{LayerNorm}(x + \text{Sublayer}(x))$

• Residual Connection(Skip Connection)
  • input $x$ 의 함수 return 값 $f(x)$ 에 대해, input $x$을 다시 더해줌
  • 경험적으로, Residual connection을 적용했을 경우, 학습 과정에서 더 잘 수렴하는 것으로 나타남

Decoder

Deocder의 경우는 Encoder와 같은 1) Self-Attention 2) FFN 외에 3) Encoder-Decoder Attention의 3가지 Sub-layer로 구성된 Layer를 중첩시킨 구조로 이루어져 있다 (해당 논문에서는 Layer의 수를 6으로 놓고 설계하였다).

 

Encoder와 마찬가지로, 매 Sub-layer에 대해 Residual Connection 진행

1. Self-Attention
   • Encoder와 동일
   • Decode 과정에서, 이후의 sequence의 정보를 가져와 사용하는 것을 방지하기 위해, masking을 하도록 수정
     • output embedding의 look-ahead table에 1만큼의 offset을 적용
     • 0의 embedding 값을 마스크로 사용
2. FFN
   • Encoder와 동일
3. Attention
   • Encoder Stack의 output에 대한 Multi-Head Attention 연산 진행
   • 그 외에는 다른 sub-layer와 동일

Attention

Attention 연산은 하나의 Query 벡터와 Key-Value 벡터의 쌍을 하나의 output으로 mapping하는 과정으로 이해할 수 있다.
Ouptut 벡터는 Value 벡터의 Weighted Sum으로 계산되며, 이 Weight는 Query, Key간의 연산으로부터 계산된다.

• Scaled Dot Product Attention
  1. Query, Key 벡터의 내적값(Dot product; Cosine Similarity)을 구함
  2. Scaling : Key벡터의 dimension 크기의 root값으로 나눠줌
  ------------------ Scaled Dot Product ---------------------
  3. Softmax(각 input sequence에 대한 scaled dot product에 대해)
  4. Softmax의 output 벡터와 Value 벡터의 Weighted Sum
     $ \rightarrow Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V $
  • Q,K($d_k$), V($d_v$)

Attention의 종류에는 크게 Additive, Dot product Attention이 있으며, 이론적 복잡도는 유사하지만, dot product attention의 경우에는 matrix multiplication code(np.matmul / torch.matmul)을 통해서 더 간편하게 구현할 수 있으며 메모리 효율적이라고 할 수 있다.

 

$d_k$가 작은 경우에는, Additive와 dot product의 결과가 유사하게 나타나지만, 그렇지 않은 경우에는 dot product 벡터의 dimension이 커지면서, softmax함수의 output값에 대한 gradient가 매우 작아지는 수준으로 나타나게 되기 때문에 scaling을 진행하게 된다,

- 개인적으로 생각하기에, dot product값이 매우 커지게 되면, softmax함수를 취했을 때의 output에 대한 편차가 매우 커질 수 있기 때문에(e.g. [0.999, 0.00001, 0.0002 ...]) backpropagation하는 과정에서 이를 활용한 gradient update가 제대로 이루어 지지 않아 업데이트가 잘 이루어 질 수 없다는 것으로 이해

 

Encoder-Decoder Attention의 경우,

• Q벡터는 Deocder의 이전 layer에서 가져옴
• K,V벡터는 enocder의 output layer에서 가져옴

Self-Attention의 경우,

• 동일한 Latent Space(이전 layer의 ouptut 값)에서 Q,K,V를 추출해서 사용
• 매 포지션 마다 전체 Sequence를 고려할 수 있다는 장점이 있음

Multi-head Attention

$d_\text{model}$ 크기의 Q,K,V 벡터를 가지고 한번만 Attention 연산을 진행하는 것 보다,

h번 동안 $d_k, d_k, d_v$ 크기의 Q,K,V 벡터를 서로 다른 weight를 통해 linaer projection해 구한 뒤, Attention 연산을 병렬적으로 진행하고, 그 뒤에 합치는 과정

$ head_i = Attention(QW^Q_i, KW^K_i, VW^V_i) $
$ where W^Q_i \in R^{d_\text{model} \times d_k}, W^K_i \in R^{d_\text{model} \times d_k}, W^V_i \in R^{d_\text{model} \times d_v} $
$ MultiHead(Q,K,V) = Concat(head_1, ..., head_hW^O $

• 해당 논문에서, $d_k = d_v = d_\text{model}/h = 64$를 사용

Transformer는 3가지 방법으로 Multi-head Attention을 사용

1. Encoder-Decoder Attention
2. Encoder self-attention
3. Deocder self-attention
   • Mask 적용 : Masking된 부분의 attention값을 $-\infty$으로 설정하고 softmax를 취해줌으로서, softmax값을 0에 가까운 값으로 만들어준다.

Position-wise Feed-Forward Network

Encoder, Decoder의 매 레이어 마다 ReLU함수를 activation function 으로 삼는 FFN를 추가해준다.

$ \rightarrow FFN(x) = max(0, xW_1 + b_1)W_2 + b_2 $

* Sinusoidal Positional Encoding (Reference : https://towardsdatascience.com/master-positional-encoding-part-i-63c05d90a0c3)

Positional Encoding

• Reference :
  • https://towardsdatascience.com/master-positional-encoding-part-i-63c05d90a0c3
  • https://kazemnejad.com/blog/transformer_architecture_positional_encoding/
  • https://velog.io/@gibonki77/DLmathPE

Transformer는 Convoultion이나 Recurrent 구조를 사용하지 않기 때문에, 모델이 Sequence정보를 활용할 수 있도록 하기 위해서 Encoding을 통해서 token의 Position정보를 Encoder, Decoder의 Embedding에 추가해준다.

해당 논문에서는 다음과 같이 positional encoding을 정의한다.

• 짝수인 경우
  $ PE_{pos,2i} = sin(pos/10000^{2i/d_\text{model}}) $
• 홀수인 경우
  $ PE_{pos,2i+1} = cos(pos/10000^{2i/d_\text{model}}) $

논문을 처음 읽었을 때에는 PE부분에 대한 설명은 크게 중요하지 않고 자의적으로 설정한 것이라고 생각해 개념적인 부분만을 이해하고 넘어갔지만, 이제는 조금 더 깊이 알아보고자 자세히 다뤄보려고 한다.

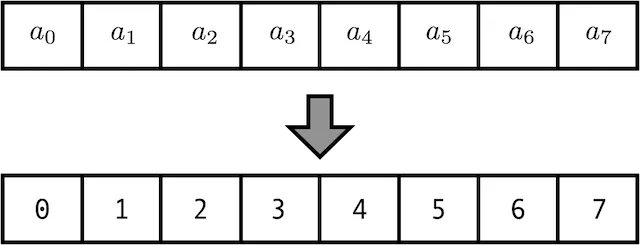
1. 단순 Count
   • 0부터 시작해서 Sequenc의 인덱스에 맞춰 차례대로 Mapping
   • 문제점
     • Sequence가 길어질수록, PE값 역시 커지게 되고 PE값이 너무 커지게 되면 NN의 weight를 학습할 때에 Exploding Gradient와 같은 문제점이 생기기 쉽다,

2. 정규화 Count
   • 단순 Count에서 전체 Sequence 길이로 나눠 정규화 진행
   • 단순 Count에서 발생하게 되는 PE값이 너무 커지는 문제점 해결
   • 문제점
   • Sequence길이가 달라지면서, Position이 서로 다름에도 불구하고 같은 PE 값을 갖게 된다,
     • 0.8이라는 PE값을 갖는 경우,
       • Sequence = 5 : Position = 4
       • Sequence = 20 : Position = 16

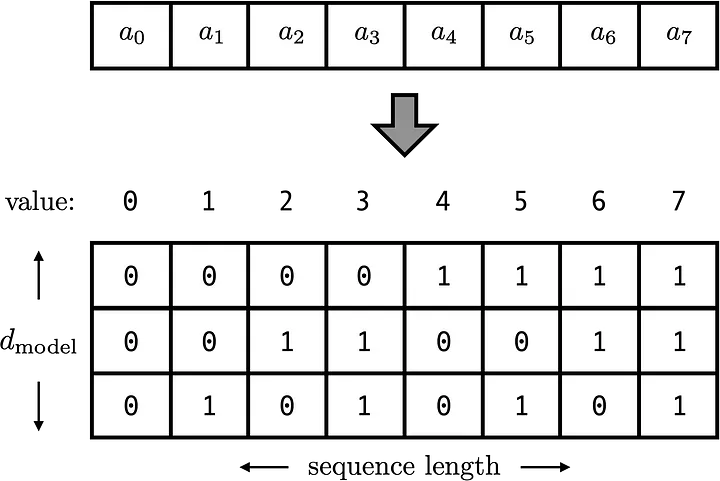
3. 이진수

1,2번의 문제점을 보완하기 위해, 십진수 대신 이진수를 PE값으로 적용해보자

• 1,2의 방법과 마찬가지로 전체 Sequnce에서 각 Position이 서로 구별되고,
• Vector화 하기 때문에 1번과 같은 Exploding Gradient에 대한 위험도 적을뿐더러,
• Sequence의 길이가 달라진다고 하더라도, Unique한 PE값을 가지게 되므로 2번 방법의 문제점 역시 보완 가능하다.
• 문제점
  • Encoding값의 불연속성
  • 참고한 포스트의 표현에 의하면, 밑의 부분으로 인해 문제가 발생한다.

Our binary vectors come from a discrete function, and not a discretization of a continuous function.

|Continuous|Distance|
|$0 \rightarrow 1$|$1$|
|$1 \rightarrow 2$|$1$|
|$2 \rightarrow 3$|$1$|

|Discrete|Distance|
|$0 \rightarrow 1$|$1$|
|$1 \rightarrow 2$|$\sqrt{2}$|
|$2 \rightarrow 3$|$1$|

• 위와 같이, 연속적인 경우에는 각 PE사이의 거리가 일정했지만, Binary Vectorize한 경우에는 거리가 일정하지 않아 PE의 일관성이 부족하다는 문제점이 생기게 된다.

4. 연속성을 가진 Binary Vector의 사용

3번의 문제점을 보완하기 위해, 불연속적인(Discrete) Binary Vector를 연속적인(Continuous) Binary Vector로 바꿔보려 시도하게 된다.

이진수 벡터의 성질은 그대로 유지해야하기 때문에 0과 1의 주기를 갖는 함수, 즉 삼각함수를 사용해보고자 하는 아이디어를 떠올릴 수 있다.

우선 Sine함수를 생각해보면, -1에서 1사이의 값을 갖는 주기가 반복되기 때문에 정규화와 이진 벡터의 성질을 모두 만족시킬 수 있을 뿐더러, 연속성 까지 만족시킬 수 있게된다.

이를 직관적으로 이해해 보자면,

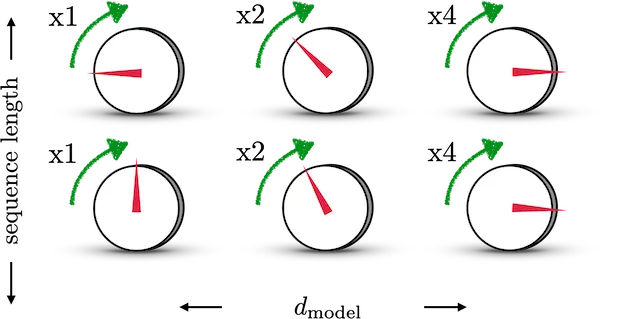
위 그림을 이진 벡터와 동일하게 놓고 생각해보자, 각 Row는 하나의 Sequence(Position)이고, 각 Column은 Vector의 Dimension이다.

첫번째 Column 다이얼의 경우, 이진수의 첫번째 자리수 즉, $2^0$에 해당하는 부분으로, 첫번째 Column의 다이얼을 돌려 Off에서 On으로 바꿀때 0에서 1로 변화한다고 할 수 있으며, 0과 1사이의 값을 조절하는 다이얼로 이해할 수 있고,

두번째 Column 다이얼의 경우, 이진수의 두번째 자리수 즉, $2^1$에 해당하는 부분으로, 첫번째 Column의 다이얼을 돌려 Off에서 On으로 바꿀때 0에서 4로 변화한다고 할 수 있으며, 0과 4사이의 값을 조절하는 다이얼로 이해할 수 있다.

이러한 로직을 삼각함수에 적용시키게 되면, 첫번째 dimension의 경우, $\pi/2$, 두번째 dimesion은 $\pi/4$ ... 의 Frequency(진동수)를 갖는 삼각함수로 이해할 수 있다,

즉, dimension의 수가 커질수록, sine함수의 주기가 길어지는 형태를 띄게 되며, Postional Encoding Matrix를
$ M_{ij} = sin(2\pi/2^i) = sin(x_iw_j) $와 같이 표현할 수 있게 된다.

위 이미지와 같이, 첫번째 sine 함수가 $0\rightarrow1\rightarrow0$로 변화할 때, 두번째 sine함수는 $0\rightarrow1$로 변화하고,

두번째 sine 함수가 $0\rightarrow1\rightarrow0$로 변화할 때, 세번째 sine함수는 $0\rightarrow1$로 변화하는 방식으로 이

어진다.

이처럼, 각 dimension별로 주기가 2배씩 길어지도록 sine함수를 구성하면,

$\begin{pmatrix}

0 & 0 & 1 \\

0 & 1 & 0 \\

1 & 0 & 0 \\

\end{pmatrix}$

의 형태로 binary vector를 만들어 낼 수 있게 된다.

이렇게 하게되면, 연속성을 지닌 binary vector의 생성함수를 만들어 낼 수 있다. 하지만, 여기서도 문제점이 발생하게 된다.

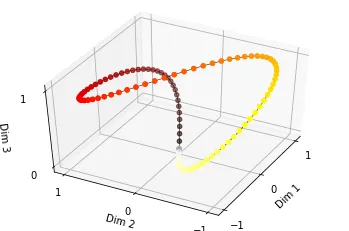
위와 같이 dimension이 3인 경우를 생각해보면, 이 함수는 closed function이기 때문에, 서로 다른 position에 대한 binary vector가 생성되더라도, 공간상에서는 비슷한 곳에 위치할 수 있다는 문제점이 생기게 된다.

 

예를 들어, 검은색에서 갈색으로 가는 부분을 dimension1에서 $0\rightarrow1$로 증가하는 부분으로 볼 수 있고, 이에 따라 dimesion2의 값이 0에서 1을 향해 점차 증가하다가 빨간색 지점에 도달할 때, dimension2는 1의 값을 가지면서 dimension1의 값은 다시 0으로 돌아가게 되는 구조로 이해할 수 있다.

 

이런 상황에서, 첫번째 sequence에 해당하는 PE는 원점인 검은색 점 근처에 형성되게 될 것이고, 마지막 sequence는 원점으로 다시 돌아오는 노란색 점 근처에 형성되게 될 것이다. 결국, 첫번째 sequence와 마지막 sequence의 PE가 매우 가까운 공간상에 형성되게 되는 것이고 이렇게 되면 제대로 된 Position 정보를 반영할 수 없게 될 것이다.

 

이러한 문제점을 해결하기 위해서, PE를 꼭 binary vector화 해서 사용하는 것이 아니라 지금까지 알아본 특성들 만을 활용해 closed case가 나오지 않도록 $minimum frequency$를 설정하고 이를 dimension이 증가함에 따라 frequency를 단조 감소시키면서, sine함수의 주기를 늘려주기만 하도록 설정하게 된다.

 

$ M_{ij} = sin(x_iw_0^{j/d_\text{model}}) $

이 수식에서, $minimum frequency$ 즉. $w_0 $을 $\frac{1}{10000}$으로 설정해주면 $j=0$일때, 주기가 가장 짧고 $j=d_\text{model}$일 때 주기가 가장 긴 삼각함수를 구성할 수 있다.

 

해당 논문에서 사용하는 $minimum frequency$는 정해진 값이 아닌, 경험적으로 가장 좋은 값을 채택한 것으로 $\frac{1}{10000}$을 사용한다,

 

두번째 문제는, 한 PE에서 다른 PE와의 관계를 정량화 시킬 수 있는 능력이 부족하는 점이다.

 

Transformer의 Attention layer는 query, key, value 벡터를 linear transformation layer를 통해 생성하게 된다.

그리고 이 과정에서 PE끼리의 관계성을 lineaer transformation layer가 잘 해석할 수 있도록 해준다면, 서로 다른 Position의 토큰 끼리의 정보를 활용하기에 더 유리할 것이다.

 

예를 들어, "I am going to eat"이라는 문장을 번역하는 Task를 진행한다고 할 때,

4번째 Position인 "eat"을 번역하는 부분에서 1번째 Position "I"의 정보를 활용하면 더 좋은 해석이 가능할 것이다.

 

이때, PE끼리의 관계성을 linear transformation layer가 파악할 수 있다면, 1번째 PE를 4번째 PE와 비슷하게 변형시켜 4번째 Position의 토큰에 대한 attention연산을 진행할 때 활용하기 용이할 것이다.

 

즉, $PE(x+\Delta x)=PE(x)\cdot T(\Delta x)$ 를 만족하는 $T$를 transformation layer가 찾을 수 있도록 PE를 구성해 줘야한다는 것이다.

 

그리고, 어떤 삼각함수의 parameter를 변화시키는 Transformation은 Rotation을 통해 발생하게 되고, sine함수를 rotation시킨 것을 반영하기 위해 cosine함수를 사용하게 된다.

 

Transformation을 위한 Rotation Matrix는

 

$ R =
\begin{pmatrix}
cos\theta & -sin\theta \\
sin\theta & -cos\theta \\
\end{pmatrix} $
로 정의되므로

 

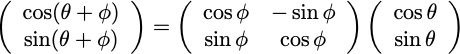
로 Rotation Transformation을 적용할 수 있게 된다.

 

최종적으로,

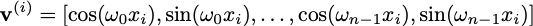
각 Row(Ppsition)이 위와 같은 벡터로 구성된 Matrix $PE$ 와

 

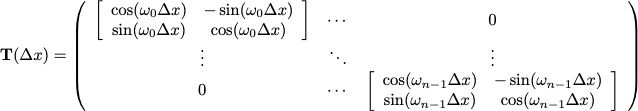
위와 같은 transformation Matrix $T(\Delta x)$를 결합해 Postional Encoding값을 구성하게 된다,