퍼셉트론
퍼셉트론이란?
다수의 입력을 받아, 하나의 신호를 출력하는 것
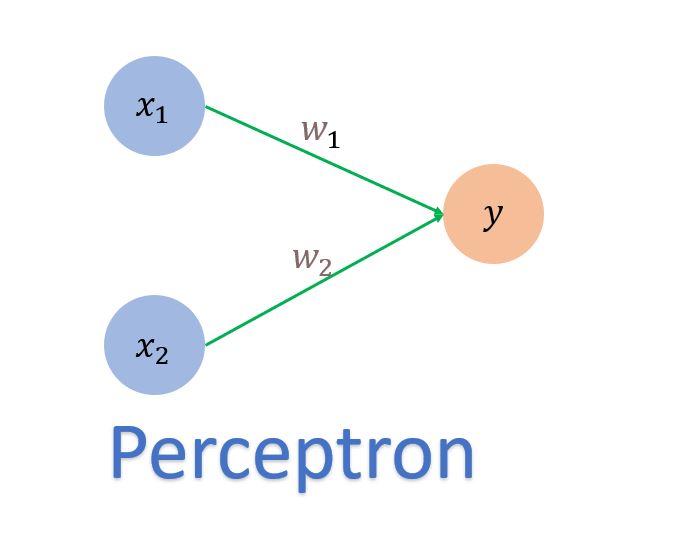
위의 그림처럼, 각 $x_{i}$노드에 해당하는 $w_{i}$의 가중합이 출력값인 $y$가 된다.
그리고 0,1의 값만을 출력하는 퍼셉트론의 경우에는 가중합을 그대로 출력하는 것이 아닌, 임계값(Threshold)를 정해 임계값 이상인 경우 1을, 그렇지 않은 경우 0을 출력하도록 한다.
이를 수식으로 나타내면 다음과 같다.
$
y = \begin{cases}
0 & (w_1x_1+w_2x_2\leq\theta) \\
1 & (w_1x_1+w_2x_2>\theta)
\end{cases}
$
이와 같은 특징을 가진 퍼셉트론을 활용해 논리 연산도 만들어 낼 수 있다.
AND 게이트

적절한 $w$(가중치)와 $\theta$(임계값)을 설정해 $x_1,x_2$가 모두 1인 경우를 제외하고 0의 값을 출력하는 AND게이트를 만들어 낼 수 있다.
그리고, AND게이트의 매개변수값의 부호를 반대로 설정하면, $x_1,x_2$가 모두 1인 경우만 0의 값을 출력하는 NAND게이트를 만들수도 있다.
OR 게이트

마찬가지로, 적절한 매개변수(가중치 및 임계값)의 설정을 통해, $x_1, x_2$둘 중 하나의 값만 1이면 1을 출력하는 OR 게이트를 만들수도 있다.
위의 논리 게이트 예시에서 볼 수 있듯이, 퍼셉트론을 구성할 때 가장 중요한 요소는 매개변수값인 가중치와 임계값이라고 할 수 있다.
같은 input($x_1,x_2$)을 사용하더라도, 매개변수의 값의 조절만을 통해서 서로 다른 출력값을 도출해낼 수 있기 때문.
Python을 활용한 Perceptron의 구현
AND 게이트
def AND(x1,x2):
w1,w2,theta = 0.5,0.5,0.7
tmp = x1*w1 + x2*w2
if tmp<=theta:
return 0
else:
return 1NAND 게이트
def NAND(x1,x2):
w1,w2,theta = -0.5,-0.5,-0.7
tmp = x1*w1 + x2*w2
if tmp<=theta:
return 0
else:
return 1OR 게이트
def OR(x1,x2):
w1,w2,theta = 0.2,0.2,0.1
tmp = x1*w1 + x2*w2
if tmp<=theta:
return 0
else:
return 1이처럼 출력을 계산하는 부분이 동일하더라도, 매개변수의 값만 다르게 바꿔줌으로써 다른 논리 연산자를 구현할 수 있는 것을 확인할 수 있다.
가중치와 편향
$y$값을 계산하는 식에서, 편향의 개념을 도입하면 식을 조금 수정할 수 있다.
원래의 식은
$
y = \begin{cases}
0 & (w_1x_1+w_2x_2\leq\theta) \\
1 & (w_1x_1+w_2x_2>\theta)
\end{cases}
$
이지만, $\theta$를 $-b$로 치환하고 정리하면,
$
y = \begin{cases}
0 & (w_1x_1+w_2x_2+b\leq 0) \\
1 & (w_1x_1+w_2x_2+b>0)
\end{cases}
$
로 다르게 표현할 수 있다.
가중치와 편향을 조금 더 해석적으로 표현하자면, 다음과 같이 표현할 수 있다.
- 가중치
- 입력 신호($x_i$)가 출력값에 주는 영향력(중요도)를 조절하는 매개변수
- 편향
- 뉴런이 얼마나 쉽게 활성화 되는지를 조절하는 매개변수
- $b = -0.1$인 경우, 가중합이 0.1만 넘더라도 뉴런 활성화
- $b = -20$인 경우, 가중합이 20을 넘어야만 뉴런 활성화
- 뉴런이 얼마나 쉽게 활성화 되는지를 조절하는 매개변수
퍼셉트론의 한계
지금까지 살펴본 AND,NAND,OR 게이트는 퍼셉트론으로 표현이 가능하다.
하지만, $x_1, x_2$중에서 하나만 1인 경우에 1을 출력하도록 하는 XOR게이트의 경우에는 하나의 퍼셉트론으로 표현이 불가능하다.
위의 3개의 Gate를 시각적으로 표현하면 다음과 같다.
매개변수(weight & bias)와 Input의 가중합을 나타내는 선형의 식으로 0,1의 출력값에 대한 영역을 구분할 수 있게 되는 것이다.

하지만, XOR 게이트의 경우에는 다음과 같이 구분되기 때문에, 위의 세개의 게이트와 다르게 직선으로 0,1의 영역을 구분할 수 없다.

그렇기 때문에, XOR게이트는 매개변수와 input간의 선형적인 결합을 나타내는 Perceptron으로는 표현할 수 없게 되는 것이다.
해결 방법
선형적으로 구분할 수 없다면, 비선형적으로 구분하게 만든다면 해결이 가능하다.

위와 같이 비선형적인 식으로 매개변수와 input사이의 관계를 표현할 수 있다면, XOR에 부합하는 0과 1의 영역도 구분이 가능할 것이다.
그렇다면, 어떻게 비선형적으로 영역을 구분할 수 있을까?
MLP
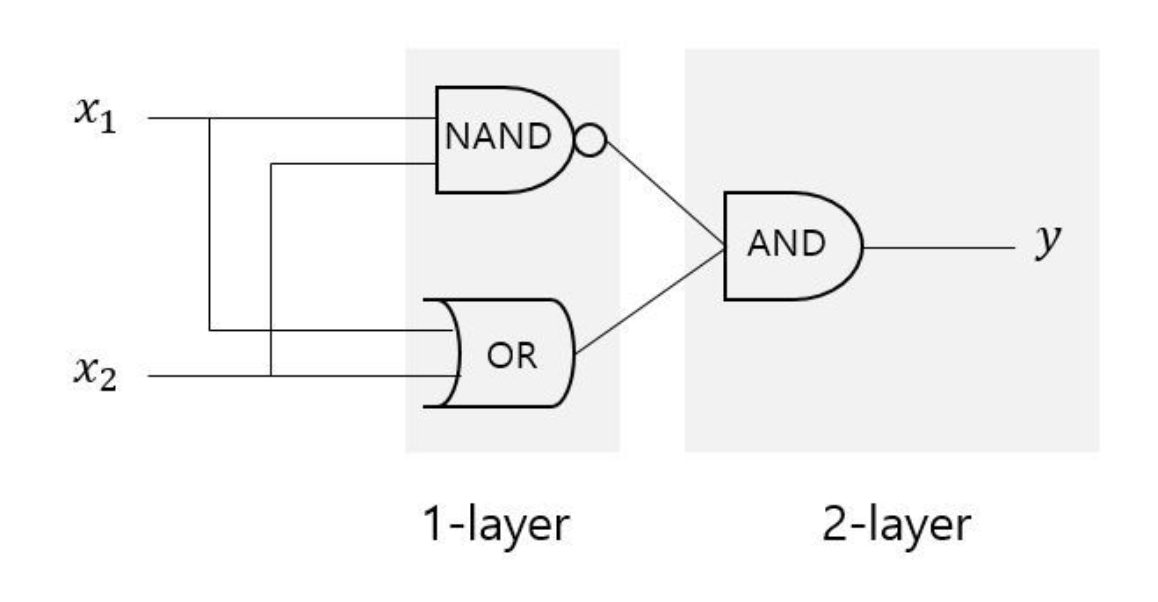
위의 그림과 같이 [AND, NAND, OR] 게이트를 적절히 조합해서 층(layer)을 2개이상 쌓으면 비선형적인 영역을 만들어낼 수 있다.
이와 같은 형태를 여러개의 층으로 쌓인 Perceptron 즉, MLP(Multi-Layer Perceptron)이라고 한다.
번외(개인적인 의문점)
여기서 들었던 의문점은 선형적으로 영역을 나누는 Gate를 조합하는 것이 어떻게 비선형성을 보장할 수 있냐는 것이었다.
처음으로 생각했던 것은, Activation Function이다. Neural Network를 구성할때 가장 중요한 점은 Non-Linear한 Activation Function을 넣어줌으로써, Network의 출력이 단순 가중합으로 계산되는 것이 아니라 비선형적으로 Mapping되도록 하는 것이다.
그렇기 때문에, XOR 게이트의 Activation Function인 Step function으로 인해, 비선형적으로 영역을 나누는 것이 아닐까 생각했지만, 다른 논리 게이트들 역시 Step Function을 사용하고 있음에도 선형적으로 영역을 구분하기 때문에 이는 아닐 것이라는 생각이 들었다.
관련 자료를 찾아보던 중
Multi-layer perceptron as a non-linear classifier — 03
Motivation
medium.com
MLP에 대한 내용을 다루는 해당 포스트에서 관련 내용을 찾을 수 있었고, 이에 대한 나의 생각을 정리해보면 다음과 같다.
- Activation Function은 연산된 값을 비선형적으로 Mapping 시키는 용도이므로, 영역을 선형적으로 나누는 것과는 직접적인 관련이 없다.
- AND, NAND, OR 게이트에서 선형적으로 나눠지는 이유는 Input과 Weight의 가중합이 Linear Combination이기 때문이다.
- XOR게이트가 비선형적으로 영역을 나누는 이유는 여러개의 Linear Combination을 다시 결합시킨 구조이기 때문이다.
- Decision Tree가 비선형적으로 데이터를 분류하는 것과 비슷한 개념으로 이해할 수 있음
결론
지금까지 살펴본 Perceptron과 MLP를 활용하면 컴퓨터를 만들어 낼 수 있을 정도로, 그 활용도가 다양하다고 할 수 있다.
'ML,DL' 카테고리의 다른 글
| 밑러닝 - (2) (2) | 2024.11.14 |
|---|---|
| Gradient Clipping (0) | 2024.08.12 |
| Ensemble - Bagging, Boosting, Stacking (0) | 2023.03.08 |
| Optimization - Cross validation, Bias & Variance, Bootstrapping (0) | 2023.03.08 |
| Random Forests (0) | 2021.09.03 |


